At point A:
$ P_{A,\ dB}=P_{TX,\ dB}\\ P_{TX} = 8 W\\ $
Using the conversion formaula for linear power to dB power,
$ P_{TX,\ dB}= 10log_{10}(P_{TX})\\ = 10log_{10}(8000)\\ =39\ dBm $
At point B:
$ P_{RX,\ dB}=P_{B,\ dB}\\ P_{B,\ dB} = P_{A,\ dB}+L_{Ch}\\ =39+ (-6)\\ =33\ dBm $
Using the conversion formaula for dB power to linear power,
$ P_{RX}=(10)^{\frac{P_{RX,\ dB}}{10}}\\ =(10)^{\frac{33}{10}}\\ =2000\ mW $
Refer to the following diagram of a communication system. Calculate power values at various stages as indicated.
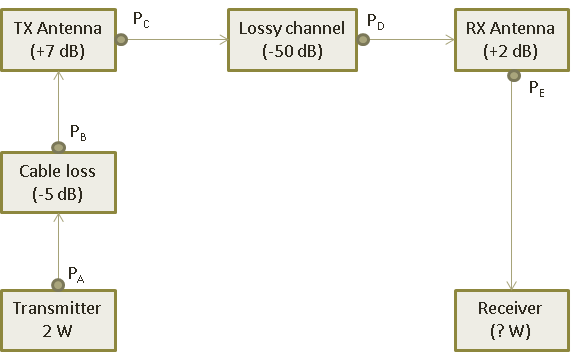
First, let's calculate power value at A in dBm.
$ P_A=10log_{10}(2)\\ =33\ dBm $
At point B:
$ P_B=P_A+(-5)\ dBm\\ =33-5\ dBm\\ =28\ dBm $
At point C:
$ P_C=28+(7)\ dBm\\ =35\\ dBm $
At point D: $ P_D=P_C+(-50)\ dBm\\ =35-50\ dBm\\ =-15\ dBm $
At point E:
$ P_E=P_D+(2)\ dBm\\ =-15+2\ dBm\\ =-13\ dBm $
$ Received\ power= P_E\\ =-13\ dBm\\ =(1/10)(1/2)\ mW\\ =0.05\ mW $