Communication Math

Khaled Mahmud

---

Data Rate, Throughput

---

Q1.

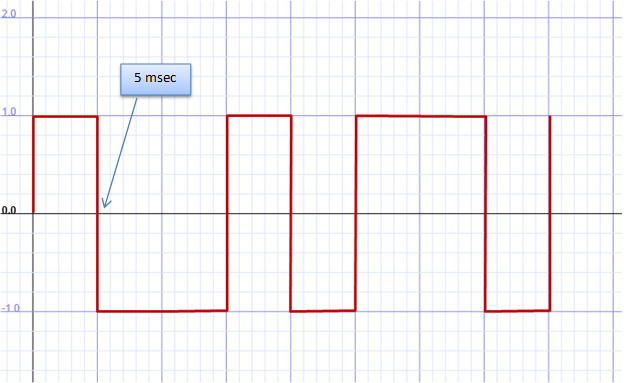
In the following NRZ-L coded signal, 8 bits of an ASCII character is represented. (a) What is the character? What is the binary value of the code? (b) If this were from NRZ-I coding, what would have been the binary value of the data? (c) If major tick intervals in x-axis represents 5 msec, what is the bit rate of this data signal?

---

Solution

(a) For NRL-L line coding, +ve voltage represents 1 and -ve voltage represents 0. The code in the image is 10010110 (150). From ASCI chart this code represents û.

(b) For NRZ-I, any change of signal level indicate 1. No change means 0. So with NRZ-I encoding, the bits will be (from first transition), 10111011 (187). Again from ASCII chart this code represents ╗.

(c) Bit rate and bit period is related by

$ R_b=\frac{1}{T_b} $

Tb=5*10**(-3)            # Bit period, in sec
Rb=1/Tb        #Bit rate, in kbps
print('Bit Rate: ',Rb, 'bps')
print('Bit Rate: ',Rb/1000, "kbps")

Bit Rate:  200.0 bps
Bit Rate:  0.2 kbps

---

Q2.

One network interface card is capable of sending data at a rate of 5 Mbps. (a) What is the bit duration (also called bit period) of the data? (b) If the data is grouped into frames of 1 kB, what is the frame rate?

Solution

(a) Bit period is the inverse of bit rate.

$ R_b=\frac{1}{T_b} $

Rb=5*10**(6)
Tb=1/Rb
print('Bit duration= ',Tb, 'sec')
print('\t\t=',Tb*10**(6), 'μsec')   #microsec
print('\t\t= ',Tb*10**(9),'nanosec')

Bit duration=  2e-07 sec
		= 0.19999999999999998 μsec
		=  200.0 nanosec

(b) Frame size in bits, FB= Total bits in a frame
Frame duration, Tf = (Frame size in bits) x (Bit duration)
Frame rate, Rf =1/(Frame rate)
Note:
1 kByte = = 1024 x 8 bit = 8192 bits

FB=1 *1024; # in bytes
FB= FB*8;   # in bits
Tf=FB*Tb;
Rf=1/Tf;    # in frame per sec (fps)
print('Bit Rate: ',Rf, 'fps')

Bit Rate:  610.3515625 fps

---

Q3

A certain transceiver pair can transmit and receive data signals at a rate of 10 Mbps. Data is send by fixed frames of size 50 bytes each. However, out of these 50 bytes, only 40 bytes are user data, the rest of the frame is overhead. What is the throughput of the user data?

Solution

\begin{equation*} Throughput=\frac{Net\ data\ per\ frame}{Gross\ data\ per\ frame}Data\ rate \end{equation*}

Rb=10;          # Data rate in Mbps
FB = 50;        # Frame size in bytes, gross
FBn = 40;       # Net data transmitted per frame
Tp = (FBn/FB)*Rb;    #Throughput, in Mbps
print('Throughput =',Tp, 'Mbps');

Throughput = 8.0 Mbps

---

Q4.

Using digital circuit switched (CS) telephone system, you and your friend talked for exactly 10 minutes. How much total data (in units of bytes) flew in both directions of this duplex link? Ignore the setup data. Assume toll quality (64 kbps) circuit.

Solution

Given,
Total talk time = 10 min
Data rate in each direction = 64 kbps
Total data transfered = Talk time

\begin{equation*} Total\ data\ transfered=(Talk\ time)\ x\ (Data\ rate) \end{equation*}

Rb=64;                         # in kbps
TalkTime=10 * 60;              # in second
TxData= TalkTime*Rb*1000;      # in bits
TxData = TxData/(1024*8);      # in kByte
print('Data transferd per direction: ',TxData, 'in kByte');
TxData =2*TxData/1024;
print('Total data transferd in both direction: %5.2f in MByte' % TxData);

Data transferd per direction:  4687.5 in kByte
Total data transferd in both direction:  9.16 in MByte

---

Q5.

Using FTP, you are downloading a 20 MB file using a 5 Mbps link. How long will it take to download the file? Assume 25% overhead for FTP protocol.

Solution

Given,
R_b=5 Mbps
User Byte=20 MB
FTP overhead=25%

Total FTP data (including the overhead), FtpData =20x(1+0.25) = 25 MB

\begin{equation*} Transmission\ duration,T=\frac{FtpData}{R_b}=\frac{(25x1024x1024)x8}{5x1000000}sec=41.94\ sec \end{equation*}

Rb=5*(10**6);                   # Bit rate in bps 
FtpData=20*(1+.25);             # Data in MB
FtpData=FtpData*1024*1024*8;   # Data in bits
T=(FtpData/Rb);                # Transmission time in sec
print('Transmissio time= %8.2f sec' % T);

Transmissio time=    41.94 sec

---

Q6.

You are sending a frame of 1000 byte across a 500 m coaxial cable in a 10 Mbps link. How long will take for the last bit to arrive at the receiver, from the start of the transmission?

---

Solution

R_b=10 Mbps
Distance,d=500 m

Data,D = 1000 B = 8000 bit
Assuming speed of signal in coaxial cable=2x10⁸ m/s
Note: You can use speed of light as well, if you are not given the speed in coaxial cable.

Time for the first bit to arrive is same as the propagation delay.

$$ \begin{aligned} &Propagation\ delay, T_p=\frac{distance}{speed}=\frac{500\ m}{2x10^8\ m/s}=2.5\ μsec \\ &Frame\ duraton,T_F=\frac{D}{R_b}=\frac{8000}{10x(10)^6 }=800 μsec \\ \end{aligned} $$

Total time of transmission, the start to end is the sum od these two values. $$ \begin{aligned} &T= T_P+T_F=2.5+800=802.5 μsec \end{aligned} $$

Rb=10;           # Data rate, in Mbps
d=500;           # length of cable, in m
D=1000;          # Data in byte
B=8000;          # in bit 
c= 2*(10**8);    # speed of transmission through copper cable, in m/sec

Tp = (d*10**6)/c;     # Propagation delay, μsec
Tf=B/Rb;             #Frame duration, μsec
Ttotal=Tp+Tf;        # total time, in μsec
print("Propagation delay= %5.2f μsec" % Tp);
print("Frame duratoin= %5.2f μsec" % Tf);
print("Total time= %5.2f μsec" % Ttotal);

Propagation delay=  2.50 μsec
Frame duratoin= 800.00 μsec
Total time= 802.50 μsec

---

Q7.

The machine in the diagram below is transmitting one of the 4 symbols every 10 microsec. With an alphabet of 4 symbols the machine can send 2 bits per symbol.

1. What is the symbol rate?
2. What is the bit rate?
3. What sequence of symbols would you transmit to send:
   1. 10010110
   2. ASCII code of the letter ‘A’. (use 8 bits)

---

Solution

(1) $ Symbol\ rate, R_S=\frac{1}{10x10^{-6} }=0.1\ Msymbol/sec $
(2) $ \begin{aligned} &Symbol\ per\ bit,r=2 \end{aligned} $
$ \begin{aligned}\\ &Bit\ rate,R_b=(Symbol\ rate)x(Symbol\ per\ bit)=rR_S=2x0.1=0.2 Mbps \end{aligned} $

(3) (A) The transmitter will pick 2 bit from queue and convert them into one symbol: 10 01 01 10

Symbol 1	Symbol 2	Symbol 3	Symbol 4

(B) Ascii code of A is 01000001: Arranging in 2 bits= 01 00 00 01

Symbol 1	Symbol 2	Symbol 3	Symbol 4

---

Q8.

A packet with 100 kB is being sent from a base station to a mobile station. The distance between the tower and the mobile station is 2 km.

1. How much time will it need for the first bit to arrive at the receiver?
2. How long will it take for the full packet to be received at the receiver? Data rate is of the channel is 10 Mbps.

Solution

(1)

$ Data\ length,D=100 kB=100x1024x8 bits \\ Propagation\ delay,\ T_P=\frac{distace}{speed}=\frac{(2000\ m)}{(3x10^8\ m/ses)}=6.67\ μsec $

(2)

$ Frame\ duratioin,\ T_F=\frac{100x1024x8}{(10x10^6 )}=81920\ μsec \\ Total\ time,\ T= T_P+\ T_F=(6.67+81920)=81926.7\ μsec $

---

---

Q9.

One mobile game sends status update to the server once in 0.5 second. On average, this status update message from the game application has a size of 1 kB. The lower layer protocol (TCP, IP, MAC) adds extra 200 bytes of header (and trailer). On average, how much bandwidth (bit rate) is consumed by this game?

Solution

Total data required in the air interface to send one message

$ \begin{aligned} &=8(1024+200)\\ &=9792\ bits \\ \\ Data\ rate =\frac{Data}{Time}\\ =\frac{9792\ bit}{0.5\ sec}\\ =19584\ bps\\ =19.58\ kbps \end{aligned} $

---

Back to Index