Communication Math

Khaled Mahmud

Error Rate, Channel Coding

Q1.

While testing a communication system, you transmitted 500000 random bits. At the receiver end you found that 30 bits are flipped (1 became 0 or 0 became 1). What is the bit error rate (BER) of the system?

Solution

$ \begin{aligned} Bit\ Error\ Rate,\ BER\ &=\frac{Number\ of\ bits\ in\ error}{Total\ bits\ transmitted}\\ &=\frac{30}{500000}\\ &=6x10^{-6} \end{aligned} $

Q2.

While testing another communication system, you transmitted 5,000,000 generated packets (frames), each of 100 bytes long. At the receiver end, you found that 200 packets are in error (have one or more bits of error).

(a) What is the packet error rate (PER)? Hint: the formula for PER is (no. of packets with error)/(total no of packets).

(b) For this communication system, do you think the BER and PER will be same? Explain.

Solution

(a)

$ \begin{aligned} Packet\ Error\ Rate,\ PER\ &= \frac{Number\ of\ packets\ that\ has\ one\ or\ more\ bit\ error}{Total\ numner\ of\ packets\ transmitted}\\ &=\frac{200}{50000000}\\ &=4x10^{-5} \end{aligned} $

(b)

No.

PER is always higher than BER, as even one bit error in a packet will corrupt the whole packet.

Q3.

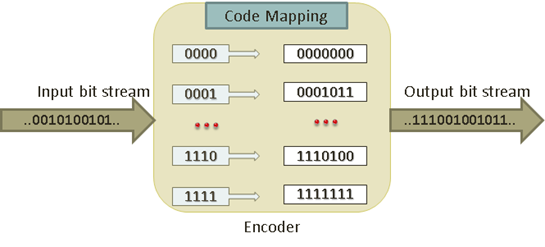
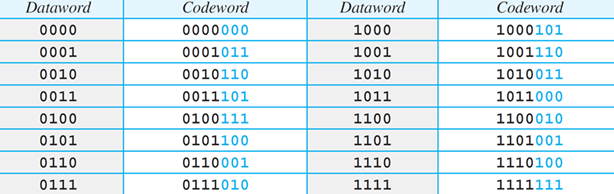
A communication system uses an encoder that takes 4 input data bits (dataword) and generates 7 output code bits (codeword). The encoder schematic diagram and complete dataword to codeword mapping table is given below.

(a) What will be the output bit stream, if the input bits are {0011010111000001}?

(b) For a particular receiving session, if the decoder receives {10110000011101}, what datawords were actually sent?

(c) If the input stream has a bit rate of 64 kbps, what should be the minimum output bit rate? Show your work.

Solution

(a)

First, divide the input bits into groups of 4 bits. We have 4 datawords. 0011010111000001 = 0011 0011 1100 0001

Then use the mapping table to encode the datawords into codewords

0011 = 0011101

0011 = 0011101

1100 = 1100010

0001 = 0001011

So, the output bit stream will be, combining all codewords serially,

0011101001110111000100001011

(b) Given,

Received sequence of codeword= 10110000011101

Dividing the sequence into groups of 7 bits, we get 2 codewords.

1011000 0011101

Now, using the mapping table, we can find the corresponding data word.

1011000 = 1011

0011101 = 0011

(c) The data rate of input bit stream is 64 kps.

However, the encoding process increases the amount of data with a factor of (7/4)

Therefore, the required data rate can be calculated as follows.

$ \begin{aligned} R&= 64 x (7/4)\\ &=112\ kbps \end{aligned} $

Q4.

Following diagram show how GSM user data at 9.6 kbps is encoded and transmitted. Calculate the transmitted data rate.

Solution

The system is transmitting 456 bit in every 20 msec.

$ \begin{aligned} R_b&=\frac{Bits}{Duration}\\ &=\frac{456\ bit}{20\ msec}\\ &=22.8\ kbps \end{aligned} $

Back to Index