1. Bit Rate and Bit Period relation:¶
The relation between bit rate and bit period is given by the following relation. Similar relation applies to symbol rate and symbol period.
$ R_b=\frac{1}{T_b} $
2. Bit Rate and Symbol Rate relation:¶
For an M-ary (level) modulation scheme, the relation between symbol rate and bit rate is given by the following. Here is r is bit per symbol.
$ R_b=rR_s\\ r=log_2 (M) $
3. Shannon’s capacity theorem:¶
The capacity (data rate) of a communication system isdetermined by the power of the signal, and bandwidth and noise of the channel.
The relation is given the following formula. If BW is in Hz, then C will be in bps. (Note: SNR here is the ratio of signal power to noise power in linear scale, hence dimensionless).
$ C=(BW)log_2(1+\frac{P_S}{P_N})\\ SNR=\frac{P_S}{P_N} $
4. Throughput:¶
It is the net amount of data that flows through a system. In calculating throughput, the overhead (or the extra information need to successful communication) is not included. Only the actual data, depending on for which layer we are calculating the throughput for, considered. For example, if we are calculating throughput in IP layer, any overhead below IP layer (e.g. Ethernet header, physical layer overhead) should not be counted. This means we need to figure out how much data in terms of IP packets is being transmitted.
5. Nyquist sampling rate:¶
The minimum sampling rate required to reproduce signal without any loss of information is twice the highest significant frequency of the signal. If the highest frequency (significant) content of a signal is fH, then the minimum sampling rate is 2fH.$ Nyquest\ rate=2f_H $
6. Base-2 Log¶
You can calculate logarithm of base 2 using this relation.
$ log_2(x)=\frac{log_{10}(x)}{log_{10}(2)} $
7. Decibel (dB and dBm) Calculation:¶
(i) dB: Relative Power: Ratio of Output Power to Input Power: Loss or Gain in the Channel¶
$
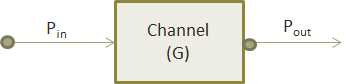\begin{aligned}
G_{dB}=10log\frac{P_{out}}{P_{in}}\\
\end{aligned}
$
(ii) dBm: Absolute Power: Output Power with respect to 1 mW¶
$
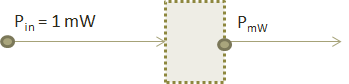P-{dBm}=10log(P_{mW})\\
$
(iii) Converting from Log Scale to Linear Scale¶
$ P_{mW}=(10)^{\frac{dBm}{10}}\\ $
(iv) Output Power After Loss of Gain¶
$
P_{out,\ dBm}=P_{in,\ dBm}+(Loss\ or\ Gain)_{dB}
$
Note: Loss is expressed as negative gain
Times 10 Relation
| Linear (mW) | Log (dBm) |
|---|---|
| 1 mW | 0 dBm |
| 10 mW | 10 dBm |
| 100 mW | 20 dBm |
| 1000 mW | 30 dBm |
| 0.1 mW | -10 dBm |
| 0.01 mW | -20 dBm |
Times 2 Relation
| Linear (mW) | Log (dBm) |
|---|---|
| 1 mW | 0 dBm |
| 2 mW | 3 dBm |
| 4 mW | 6 dBm |
| 8 mw | 9 dBm |